Nonlinear Differential Equations...

I stumbled upon a very useful program today called Octave. It is a high-level numerical oriented programming language that is somewhat similar to MATLAB. After many hours of tweaking the settings, downloading files, and writing some functions that write other functions, I've stumbled upon some interesting preliminary findings. Basically, I wrote a program that generates systems of nonlinear ordinary differential equations randomly. Then I used the built-in numerical integrator to see what the behavior of these functions looks like. In this first graph, lines 1-3 are the time solutions of the variables x,y, and z with the initial conditions (0,0.3,0.1). I checked for longer times of integration and it appears that the system eventually converges on a fixed point. The initial behavior of the system is very interesting, because it acts very similarly to a damped oscillator. Yet another interesting aspect is we can see that the variables x and z are out of sync up until around 5000 time units, and then they suddenly come right into harmony. If this is not order for free I do not know what is!















The next image is the phase space of the x and y dimensions. This is a very interesting pattern, it looks sort of like a wing or a leaf. The magnitude of the time solution of the y variable is very small compared to that of the x and z variables, but it still has interesting behavior.














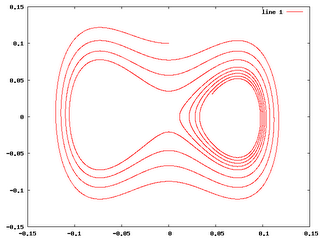
This image demonstrates the phase space of the solution along the x-z plane. It looks like there are two basins of attraction, and eventually the basin on the right determines the long term behavior of the system. The point at which the x and z variables come into sync is probably when the function reaches an "event horizon" where it is forced to enter the basin of attraction on the right.














Finally, this last image is the phase space in the y- z plane. This is a totally different pattern, that brings to mind a cell under going mitosis. The dynamics of this system of non-linear differential equations is obviously very complicated, but there do seem to be some underlying patterns that govern the entire system. Hopefully I will be able to develop a more systematic system for identifying these underlying patterns as well as finding that elusive beast of emergence.